Математическая статистика и прогнозы когда данных мало

Оригинал тут → https://searchengines.guru/ru/articles/23790

Для правильного назначения ставок важно как можно точнее вычислить вероятность конверсии для каждого ключевого слова. Однако, при небольшом числе кликов, показателю конверсии нельзя доверять — он обладает значительной погрешностью. В этой статье я приведу несколько простых методов повышения точности оценки вероятности конверсии.

Вероятность

Не следует путать показатель конверсии с ее вероятностью. Например, если у нас 1 клик и 0 конверсий, то показатель равен нулю, но это не значит что и вероятность покупки тоже нулевая.

Вероятность по определению — это частота на бесконечности. Другими словами, если бы число кликов было бы бесконечно большим, то показатель и вероятность конверсии были бы равны. При большом числе кликов эти два числа примерно равны. Но при малом — они могут существенно отличаться.

Погрешность

Благодаря теории вероятности, легко вычислить среднюю погрешность которую имеет показатель конверсии. Это число показывает, на сколько, в среднем, показатель конверсии отличается от ее вероятности:

σ=√((p(1-p))/n)

Где p вероятность конверсии, n — число кликов. Например, при конверсии = 1% и 100 кликах мы получаем

σ=√((1% * 99%)/100) ≈0.995%

На первый взгляд, это небольшая погрешность, но искомое число (вероятность конверсии) тоже мало и по условиям примера равно 1%. Другими словами, при 100 кликах погрешность примерно равна показателю конверсии.

Поэтому, для наглядности, перейдем к относительной погрешности, разделив погрешность на вероятность конверсии. Получим 99.5%.

Формула для относительной погрешности:

σ/p=√((p(1-p))/n)/p=√((p*(1-p))/(p^2*n))=√(((1-p))/pn)

Мы можем рассчитать относительную погрешность в зависимости от числа кликов и показателя конверсии. Получим:

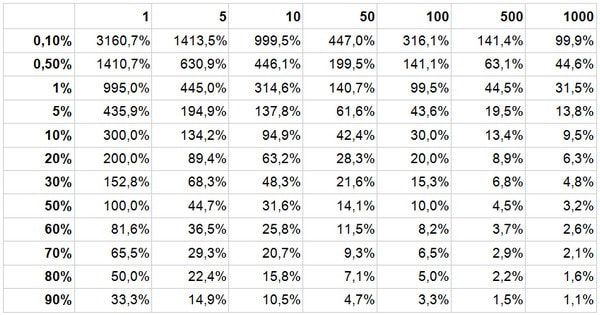
Легко видеть, что при низком числе кликов погрешность получается просто астрономической. При одном клике и 1% конверсии относительная погрешность равна 995,0%. То есть, погрешность почти в 10 раз превышает вероятность конверсии.

На самом деле это оценка погрешности снизу. В реальности погрешность будет выше, поскольку на показатель конверсии может повлиять, например, то, что по чистой случайности все 5 кликов ключевого слова произошли ночью.

Пулинг

Как мы выяснили, в большинстве случаев, полностью полагаться на показатель конверсии нельзя. Нам нужно найти дополнительный источник информации. Самый очевидный способ — использовать показатель конверсии объявления, кампании или URL.

В статистике это называется пулингом (от английского to pool — объединять). Более понятный термин — усреднение, мы усредняем данные ключевого слова и некоторой группы ключевых слов, например, объявления. Чем больше у ключевого слова кликов, тем меньше мы усредняем.

В статистике для оценки вероятности принято использовать бета-биномиальную модель. Ее, например, использует Marin Software, если верить их патенту. Мы в К50, тоже используем схожую схему.

Вероятность конверсии ≈(Конверсии + A)/(Клики + A/M )

M — показатель конверсии объявления

A — степень пулинга, некоторое число. Выражает степень сходства ключевых слов в группе.

Степень пулинга, по сути, это тот объем информации, который несет группа, и которую мы добавляем к информации ключевого слова. В статистике А принято измерять в псевдоуспехах или, в нашем случае, псевдоконверсиях. Отношение А/М это число псевдонаблюдений или, в нашем случае, псевдокликов.

В итоге эту формулу легко запомнить: конверсии + псевдоконверсии, деленные на клики + псевдоклики.

Мягкий пулинг

Теоретическая оценка снизу A=1. Что подтверждается практикой. За исключением больших интернет-магазинов, которые торгуют всем — от памперсов до холодильников. Если у них за группу принять все их ключевые слова, то оптимальный A около 0.7. И даже в этом случае, 0.7 ближе к 1 чем к 0. Следовательно, мягкий пулинг не хуже, чем полное отсутствие пулинга.

В итоге наша формула:

Вероятность конверсии ≈(Конверсии + 1)/(Клики + 1/M )

Например, в объявлении показатель конверсии равен 1%, у ключевого слова было 100 кликов и 2 конверсии. Тогда оценка будет равна (2+1)/(100+1/1%)= 3/200 = 1.5%.

Другой пример: у ключевого слова было 10 кликов и ни одной конверсии, оценка равна (0+1)/(10+ 1/1%)=1/110=0.91%

Чтобы понять адекватность этого метода, мы построим таблицу:

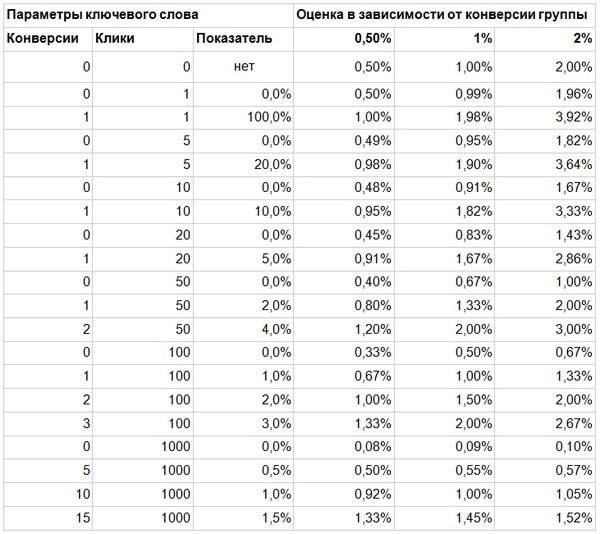
Как мы видим, оценки получаются довольно адекватными. При небольшом числе кликов, оценка — значительно лучше показателя конверсии, при большом — они почти не отличаются.

Мы можем посчитать максимальную погрешность, которая будет при мягком пулинге и сравнить ее с погрешностью без пулинга:

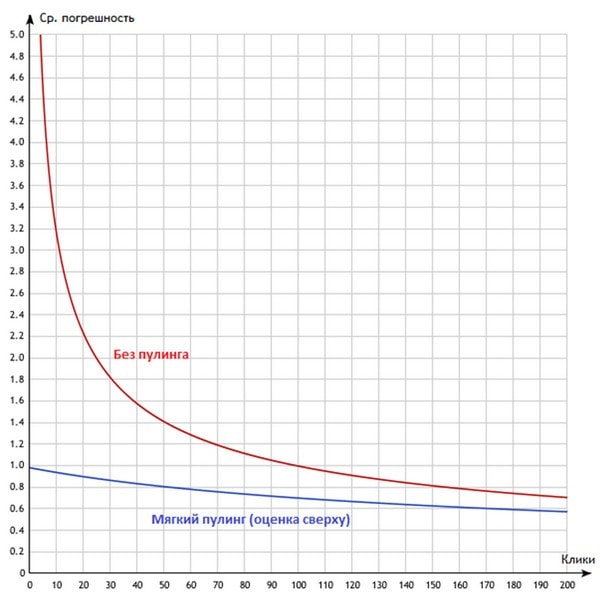
Многоуровневый пулинг

Показатель конверсии объявления тоже обладает довольно высокой погрешностью. Поэтому его тоже можно «пулить» и использовать это оценку для расчета ключевого слова.

Например, показатель конверсии у кампании 1%. У объявления 300 кликов и 2 конверсии. У ключевого слова была 1 конверсия и 70 кликов. Считаем оценку вероятности конверсии объявления (2+1)/(300+1/1%)=3/400=0.75%. Используем оценку объявления для оценки конверсии ключевика (1+1)/(70+1/0.75%)=2/203=0.985%

Таблица

По этой ссылке таблица в Google Docs, которая оценивает вероятность конверсии методом многоуровневого пулинга. Скопируйте ее себе на Google диск или сохраните как файл для Microsoft Excel.

В таблице есть четыре уровня: Аккаунт (все ключевые слова), Кампания, Объявление и Ключевое слово. Названия уровней условные. К примеру, вы можете, вместо объявления подставить URL.

Более того, можно посчитать оценку не только вероятности конверсии, но и, например, вероятность отказа. Нужно просто подставить вместо числа конверсий число отказов.

Проще всего посчитать данные по мягкому пулингу. Для этого нужно просто скопировать в таблицу данные по ключевым словам.

Также эта таблица считает погрешность, которую вы можете снизить, подобрав оптимальную степень пулинга. Для этого нужно вставить статистику по двум периодам.

В общем, чтобы подобрать степень пулинга, нужно:

Разбить данные на два непересекающихся периода. Например, весна и лето 2015 года и вставить эти данные в таблицу.
Попробовать изменить степень пулинга «Объявление->Ключевик» (H4). так чтобы минимизировать ошибку (D9)
Попробовать изменить степень пулинга «Кампания->Объявление» (F4). так чтобы минимизировать ошибку (D9)
Попробовать изменить степень пулинга «Аккаунт-> Кампания» (D4). так чтобы минимизировать ошибку (D9)
Вернуться на второй шаг и еще пару раз пройти этот цикл. И, в конечном итоге, вы найдете оптимальные коэффициенты пулинга. Это может занять до получаса, но для каждого сайта это нужно сделать один раз в жизни.
Вставьте суммарные данные за весь период, и таблица посчитает довольно точные оценки конверсии.

Ошибка (D9) даже при идеальном прогнозе никогда не будет нулевой. Дело в том, что в контрольном месяце число кликов не бесконечно велико, а мы сравниваем наш прогноз с показателем конверсии контрольного месяца, который отражает вероятность конверсии с очень большой погрешностью.

Поэтому снижение ошибки, например, с 40% до 36% повысит эффективность ставок намного выше, чем на 10%.

Регрессионный анализ

В математической статистике есть целый раздел, который изучает взаимосвязь между переменными и позволяет предсказывать значение одной переменной при наличии известных значений других. Этот раздел называется «регрессионным анализом».

Допустим, у нас конверсия равна 1%, а показатель отказов около 50%. Используя таблицу, данную в начале статьи, можно понять, что погрешность у показателя отказов в 10 раз ниже, чем у показателя конверсии при одинаковом числе кликов.

При этом, эти переменные имеют сильную обратную корреляцию. В зависимости от сайта — от 60% до 90%. Грубо говоря, это значит, что мы можем восстановить вероятность конверсии с точностью 60%-90%, зная вероятность отказов.

В общем, мы можем в несколько раз снизить погрешность оценки конверсии, благодаря добавлению информации, которую несет показатель отказов.

Но для этого нужно построить статистическую модель. Благодаря формуле полной вероятности, мы можем разложить вероятность конверсии так:

P[конверсия]=K *(1-P[отказ])

Где:

P[конверсия] — вероятность конверсии

P[отказ] — вероятность отказа

K — вероятность того, что произойдет конверсия, в случае если не было отказа.

Для простоты предположим, что K — это некоторая постоянная, одинаковая для всех ключевых слов. Это предположение может показаться довольно грубым, но на практике даже такая простая модель обладает довольно высокой точностью.

K можно оценить как:

K≈(показатель_конверсии_аккаунта)/(1 — показатель_отказов_аккаунта )

P[конверсия]≈(показатель_конверсии_аккаунта)/(1 — показатель_отказов_аккаунта ) *(1-P[отказ])

Вероятность отказа мы можем оценить с помощью пулинга. Нужно просто в таблицу, вместо числа конверсий, подставить число отказов. Далее, подставим оценку вероятности отказа в эту формулу и получим еще одну оценку конверсии. Назовем ее оценкой по отказам.

Взвешенная оценка

Оценку по отказам можно объединить с оценкой полученной из пулинга. И, таким образом, получить финальную оценку с погрешностью меньшей чем у двух промежуточных оценок. Например, так:

Финальная_оценка = w * Оценка_из_пулинга + (1-w) * Оценка_по_отказам

Где w — число от 0 до 1 и подбирается также как и степень пулинга, путем минимизации погрешности оценки. Для этого в той же таблице есть второй лист. Вы можете скопировать туда две оценки и подобрать w так, чтобы минимизировать погрешность.

Итоговая оценка будет лучше, чем пулинг, и лучше, чем оценка по отказам. Ну, по крайней мере, не хуже. Например, если оценка по отказам будет очень плохой, намного хуже пулинга, то оптимальный w будет равен 1. И итоговая оценка будет равна оценке пулинга.

Динамическое взвешивание

Проблема прошлого метода в том, что w не зависит от числа кликов. Хотя оценка из пулинга точнее для высокочастотных ключевых слов, а оценка по отказам — для низкочастотных.

Мы учли это на четвертом листе. Там тоже нужно подобрать только один коэффициент – S, относительную систематическую погрешность модели. Благодаря первому листу, оцените пулингом вероятность конверсии и скопируйте оценку и ее ожидаемую погрешность на четвертый лист. Благодаря первому листу, оцените пулингом вероятность отказа и скопируйте оценку и ее ожидаемую погрешность на четрвертый лист. Подберите настройку S таким образом, чтобы минимизировать средневзвешенную относительную ошибку.

Модель скрытых отказов

Показатель отказов занижен. Поскольку тот факт, что пользователь перешел на вторую страницу, не говорит о том, что он был заинтересован в вашем товаре или услуге. Он это мог сделать из праздного любопытства, или, не поняв, что ему конкретно предлагают.

Предположим, что существует некоторый скрытый показатель отказов. Вероятность ложно отрицательного срабатывания счетчика отказов. Когда к вам пришел незаинтересованный пользователь и счетчик отказов не определил такого пользователя.

В общем: Показатель отказов занижен. Это влияет на качество прогноза. Мы можем это влияние компенсировать, построив модель. Параметры модели можно подобрать так чтобы качества прогноза было максимально высоким.

Очевиден тот факт, что чем больше явных отказов, тем больше должно быть скрытых. С другой стороны, как и любая другая вероятность, вероятность скрытого отказа должна быть меньше 1. Поэтому можно построить следующую модель:

P[скрытый отказ] = erf(L * P[отказ])

Где L некоторая положительная константа. А erf — это функция ошибки. Она всегда меньше 1. Эта функция есть в Екселе.

В итоге получим:

Вероятность конверсии = K * (1 — P[отказ]) * (1-erf(L * P[отказ]))

Где K и L подбираются уже знакомым нам способом минимизации погрешности. Первоначальный K можно взять из прошлого метода, а в качестве начального — использовать L = 0.5. Для этого в таблице есть третий лист.

Модель скрытых отказов довольно хорошо описывает реальные данные. В ней всего два параметра. Практика показывает, что эта модель работает также хорошо, как и модели, основанные на полиноме с 4-6 параметрами.

Взвешивание по обратной дисперсии

Вот финальная схема для довольно точной оценки конверсии: Считаем пулингом (первый лист) оценку конверсии и копируем оценку и ошибку на четвертый лист. Считаем пулингом (первый лист) оценку вероятности отказа. Мы копируем ошибку на четвертый лист, а оценку —на третий лист. Считаем третий лист и копируем полную вероятность отказов в четвертый лист, как оценку вероятности отказов. Считаем четвертый лист и получаем довольно точную оценку вероятности конверсии.

Заключение

Данная схема является наиболее точной из тех, что можно посчитать вручную без специфических знаний в матстатистике.

В автоматических системах вроде К50 и Marin Software используются несколько более сложные схемы пулинга, но без элементов регрессионного анализа. Качество их прогноза, скорей всего, будет выше, чем у этой схемы, но не намного. Все эти системы экономят массу времени и избавляют от человеческих ошибок.

Мы в К50 Labs используем более сложные модели. Поэтому, оценку погрешности описанного в статье метода мы посчитали только для 1 клиента. Мы взяли 10 тысяч ключевых слов из статистики одного крупного рекламодателя и разделили данные на 3 периода: два периода по месяцу для обучения и один длиной полгода для теста.

Показатель конверсии. Мы считаем что показатель конверсии=вероятности конверсии.
Пулинг с подбором — первый лист в таблице.
Взвешенная оценка — итоговый метод из этой статьи. Но для ускорения работы подбор коэффициентов автоматический, в R Studio.
K50 Labs — это индивидуальная статистическая модель сделанная мной в R Studio. Она заточена под этот сайт. Кроме отказов были использованы следующие данные:

Текст ключевого слова (длина, число слов, наличие слов купить/цена и прочих).
CTR в спецразмещении и гарантии и их отношение (как признак горячих тематик).
Цены клика на поиске в зависимости от позиций
Время и глубина просмотра
Время добавления ключевого слова (оценка по ID)

MCMC Sampling — это примерно такая же модель, но в Stan Sampler. Считается все точнее, но нужно очень много вычислительной мощности — расчет занял 8 часов для 10К ключевых слов. Поэтому этот метод мы использует только в исключительных случаях.
Теоретический минимум возникает, поскольку у нас тестовый период не равен бесконечности и, поэтому, показатель конверсии на нем не равен вероятности. В скобках погрешность минус теоретический минимум, это число лучше отражает реальную погрешность.